未来教育高精尖创新中心

基于PISA2012数学素养测试分析框架的例题分析与思考

教育科学研究2015′10

秦春霞周慧

【摘要】PISA2012从内容、情境、能力三维度完善了数学素养评价分析框架。重点分析了PISA分析框架中数学过程与数学基本能力这一维度的特点，精选了“不确定性、数量、空间和图形”四个内容领域的三道PISA测试题，在北京市一所普通初中的初二年级学生中进行同题测试，结合数据分析，提出改进数学素养评价和中学数学教学研究的建议。

[关键词]数学素养;PISA数学素养测试分析框架;PISA例题分析

[中图分类号}G449[文献标识码}A[文章编号X1009-718X(2015)10-0046-06

綦春霞北京师范大学教育学部教授博士生导师 100875

周慧北京师范大学教育学部博士生（北京市朝阳区教育研究中心） 100875

本文为北京市“十二五”教育科学规划重点课题“以普通高中课程建设为载体，促进区域学校特色发展的研究”（ABA11020）的部分成果。

一、PISA 数学素养测试

PISA （国际学生评估项目）是由经济合作与发展组织（OECD）发起的一项国际学生评价项目，其测试对象是临近义务教育尾期（15 岁）的中学生的阅读、科学和数学素养，自 2000 年起每三年进行一次，九年为一个周期，每届主测一个素养，另两个素养辅之。该国际评价项目主要从终身学习的角度来看待

和评估教育的真谛，着重考查 15 岁中学生对于未来生活可能面临的问题情境的准备程度及习得的必备的知识技能。考查的知识技能主要包括：沟通、适应性、学习策略、弹性、时间管理、自我信念、问题解决、咨讯技能等。该国际测评项目侧重教育品质和均等研究，以学生社会经济背景和性别差异等因素作为分析学生是否享有均等受教育机会的变量。

二、2012年PISA数学素养测试分析框架

2012 年国际学生评估项目 PISA 测试的主项为数学素养（Mathematical Literacy），和 2003 年相同。笔者通过分析 OECD 官方网站发布的 PISA 2012Mathematics Framework，发现 2012 年 PISA 数学测评框架依然是三个分析维度（即数学情境、数学内容、数学过程），在数学素养概念界定和分析框架方面略有调整，具体分析如下。

（一）数学素养定义

2012 年 PISA 数学素养的定义如下：个体能够在不同情境中形成、运用、解释数学的能力，包括数学地推理、运用数学概念、程序、事实和工具来描述、解释、预测，帮助个体理解数学在社会生活中的作用，并且能够作出好的决策和判断，成为一个具有建设性、参与性、反思能力的公民。这个定义体现出三个特点：更为关注学生作为问题解决者的身份；强调情境和问题之间的有机关联；更为关注包括信息技术在内的数学工具的重要作用。

2012 年数学素养明确提出包括数学工具使用，工具包括实体计算工具和数字化设备、软件、计算器。基于计算机的数学工具使用是 21 世纪常用的一种学习方式，也将成为更加主流的方式。2012 年PISA 测试的创新之处在于增加了基于计算机的数学评价，作为一个选项提供给参与测评的国家和地区，同时在数学调查中是允许使用计算器的。计算器包括网络计算器是能够帮助学生完成测试任务的，也能够提供一些便利条件来检测纸笔测验所不能完全测试到的数学素养的一些内容。

（二）数学素养模型

2012 年，OECD 给出的数学素养模型包括三维度架构：一是情境维度即问题情境，指 15 岁学生可能面临的各种问题，具体包括个人生活的、职业的、社会性的、科学性的四种情境；二是内容维度即数学内容知识，包括变化和关系、空间和图形、数量、不确定性四大领域内容；三是过程维度即三种数学过程和七种数学基本能力，见表 1。

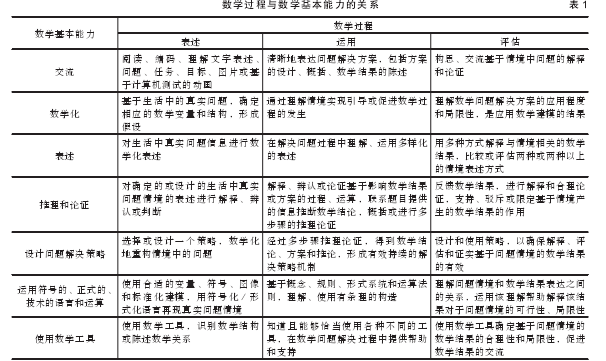
PISA2012 数学测试第一次表明该模型能够根据数学过程反馈评估结果，且该模型将为反馈评估结果提供有价值的信息，为政策制定者、教育工作者提供研究学生数学学习过程的有效资料。学生运用数学解决问题的能力是取决于在表述、运用、评估这三个数学过程的表现的。

2003 年起，摩根·尼斯（Mogens Niss）和他的丹麦同事经研究提出了八种数学能力，基本确立了2003 年 PISA 数学测试分析框架中包含的数学能力，形成数学行为评价的基本框架。2012年PISA分析框架对此作了一些修订，是基于数学专家组（Mathematics Expert Group,简称 MEG）对前几轮测试中数学能力运用情况的调查得出的，这次修订主要是将八种能力调整成了七种能力：交流，数学化，表述，推理和论证，设计问题解决策略，运用符号的、正式的、技术的语言和运算，使用数学工具。这些能力尤其体现在学生问题解决过程中，因此，也就成为数学素养测试中的重要部分。

三、基于 PISA 数学测试分析框架的例题分析

（一）基于分析框架的 PISA 例题分析

根据初中数学教学内容的特点，本研究从数学内容知识维度出发，精选了“不确定性、数量、空间和图形”四个内容领域的例题，结合 PISA 2012Mathematics Framework 中的三道原题，重点从数学过程、基本能力考查方向进行分析。为了更好地了解该题在数学能力、素养测试方面的要求，笔者在北京市一所普通初中学校随机抽取初中二年级一个普通班的学生完成了这三道题的测试，该班共有32 名学生（以下简称 A 班学生）。笔者对学生答题情况进行统计，与 2012 年 PISA 测试结果进行比较分析，具体如下。

例题 1：唱片排行榜

从例题 1 的基本信息来看，主要是考查学生读图提取信息的能力，难度很小，具体特点参见表2。

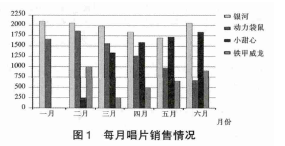
一月份，银河乐团和动力袋鼠乐团发行了新唱片。二月份，小甜心乐团和铁甲威龙乐团也发行了新唱片。下图显示的是这些乐团由一月至六月的唱片销售量（见图 1）。

1.四月份铁甲威龙卖出多少张唱片? （）

A 250 B 500 C 1000 D 1270

2. 在哪一个月份，小甜心乐团的唱片销售量首次超过动力袋鼠乐团？（）

A 没有任何月份 B 三月 C 四月 D 五月

3.动力袋鼠乐团的经理感到担心，因为他们二月到六月的唱片销售量下降。如果这个下降趋势持续，他们七月份的销售量估计是多少? （）

A 70 张 B 370 张 C 670 张 D 1340 张

第一题学生是可以直接读图回答的：找准横坐标确定月份（四月），找准纵坐标确定乐队，二者对应结合点即为乐团唱片销售数量，正确答案 B 500 张。数学过程侧重考查表述过程，从数学基本能力考查来看，题目信息明确，对 15 岁学生而言完成这道题的交流能力、设计问题解决策略能力、表述能力、读取图表信息技术能力、推理论证能力要求很低。2012年PISA测试中87%的学生答对了这道题，A班学生正确率为90.6%，略高于PISA测试答题正确率。

第二题难度稍大，需要将小甜心乐团、动力袋鼠乐团的两个数据一起读，且要比较两个乐团唱片销售情况条形图的关系，推断随着月份推移条形图的变化，细心读题才能找到正确答案 C 四月。问题解决策略则要求略高，需要将两个乐队数据进行比较，数学化过程同样需要将销售情况与图表建立直接关联，需要进行简单的推理论证。2012 年PISA测试中 78.0%的学生答对了这道题，A班学生正确率为 93.8%，明显高于 PISA 测试答题正确率。第三题比前两道题难，需要学生很好地理解图表中的数学关系，抓住关系本质，估算该乐团从二月开始每月光盘销售量平均下降的数量，并预测下一个月光盘的销售量。首先需要从图表中读取乐团每月光盘销售数据，其次估算乐团光盘销售量逐月下降的数值（300 张左右），并将此销售量下降数值运用到图表中最后一个月（六月光盘销售量约为670 张），推断保持销售量继续下降的七月销售数

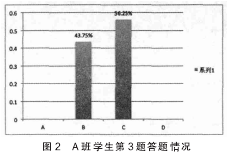
值（370 张）。本题数学过程侧重于运用，即运用图表数据进行推理分析，作出判断。设计问题解决策略方面的要求比前两题要高得多。数学化则要求从给定情境提取信息，读取多个数据，并计算出逐月下降的常量；表述能力方面使用给定图表销售量的既定趋势预测，需要有一些推理能力。整体而言题目不难，2012 年 PISA 测试中 76.0%的学生选择了正确答案 B，15.0%的学生选择了 C。A 班学生正确率仅为43.75%，56.25%均选择了选项C，远低于PISA测试答题水平（见图 2）。对“下降趋势持续”和“七月份销售量的估计”的理解，是本题的易错点，同时也考查学生从图中提取信息能力和推理能力。由此可见，A班学生在读图、预测推理能力方面有待提高。

例题 2：攀登富士山

富士山是日本著名的休眠火山，见图 3。例题2 也是来源于公开数据，考查学生从情境中抽象出数学问题和通过数学建模解决问题的能力，难度较大。具体信息参见表 3。

4.富士山只在每年的7月1日至 8月27日对外开放，这期间有 200，000 人来攀登富士山。平均每天有多少人来攀登富士山? （）

A 340 B 710 C 3400 D 7100 E 7400

5.从御殿场到富士山的登山步道长约 9 公里（km)。游客必须在晚上八点前完成来回 18 km 的路程。山本估计自己可以以平均每小時 1.5 km 的速度登山，并以两倍的速度下山。此速度的估算包含用餐和休息所花费的时间。按照山本估计的速度，他最迟要在何时出发才能在晚上八点前回来?

答：____________________________________

6. 山本带着一个计步器去记录从御殿场到登山步道所走的步数。他的计步器显示他在上山时走

了22，500 步。山本在御殿场登山步道共走了 9 km, 以公分（cm）为单位估算他步伐的平均长度。

答:____________________________________cm

第四题属于中等难度的题目，主要是根据已知

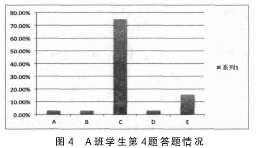
总数和特定时段，找出平均每日人数。数学过程侧重考查表述过程，通过建立数学模型找到答案。数学基本能力的设计问题解决策略要求属于中等难度，需要从题目数据中找出总天数，即七月一日到八月二十七日之间的总天数，算出平均数，需要进行一定的推理和论证。2012 年 PISA 测试中 46%的学生选择了正确答案 C，A 班学生答题正确率为75%，显著高于 PISA 测试答题水平。PISA 测试中19%的学生选择了 E 选项，A 班有 15％的学生也选择了E选项，是提取文本信息确定核心概念“总天数”出错缘故所导致的，见图 4。

第五题是给定两种不同速度、旅程总距离以及返回时间，要求答题者计算出发时间。该题数学过程侧重考查表述过程，通过数学建模找出解决问题的方案。在设计问题解决策略方面要求高，需要将几个数字建立联系，一是依据上山时间、下山时间计算平均速度，二是依据返回时间、休息时间来计算出发时间。在数学基本能力中，数学化要求较高；需要理解不同的时间（用餐时间、休息时间）及其表述、知道整个行程的流程是先上山后下山等；运用形式化、符号化、技术语言和运算能力要求较高，理解“平均每小时速度 1.5km”是答题的关键一步。因为路程是固定的（18km），上山、下山速度不一样，上山、下山所需要的时间是不一样的，计算出发的准确用时需要对题目信息准确把握，并进行很好的论证推理。2012 年 PISA 测试中只有12.0%的学生填写了正确答案“上午 11 点”，A班学生答题正确率为 56.3%，明显高于 PISA 测试学生水平，这与我国初中数学重视行程问题教学有关。

第六题陈述了距离（以 km 为单位），用距离除以步数，得到平均步伐长度（以 cm 为单位进行表示）。该题数学过程侧重考查运用过程，需要运用数字、概念、公式进行演算，涉及两个考点，一是行程问题计算，根据距离和总步数计算平均步伐，二是单位换算，难度很大。从数学基本能力考查方面来看，推理论证能力要求明显高于第四题，求平均步伐长度需要将距离与总步数建立联系，数学化要求也相对提高，准确理解生活中人行走时平均步伐长度，一般人们行走的平均步伐长度是 50cm 左右，对于推断该道题答案是有帮助的；对运用符号的、形式的、技术语言计算要求是较高的，因为两个数字单位是不统一的，需要进行单位换算。2012年 PISA 测试中只有 11.0%的学生填写了正确答案“40”，A班学生答题正确率为71.9%，明显高于PISA

测试学生水平。PISA 测试中有 4.0%的学生计算正确，而单位换算错误，将答案写成了 0.4 或 4000，这种单位换算带来的计算错误在 A 班是没有出现的，足见我国初中的基础知识教学是很扎实的。

例题 3: 修建花坛

“修建花坛”属于空间与图形领域，是生活中的真实情境问题，主要考查学生认识并计算不同图形的周长。由于是非常规图形，因此题目有一定的难度，具体特点参见表 4。

一个工匠有 32 米的材料，准备围着花园地表砌一个装饰的花坛，他正在考虑下面的花坛设计示意图。请判断在设计图里所需材料是否能用 32 米的材料完成：如认为是，请在“是”上画勾，如认为否，则在“否”上画勾（见图 5）。

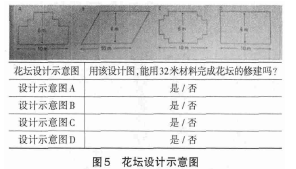
该题考查数学过程的运用，即运用数学知识、数据、程序进行推理。该题目最大的挑战是构成周长的各个线段长度不明确，要找准信息并推断出相对长度，设计解决问题方案。题目对交流能力要求主要是阅读、理解题意，将文字信息与四个设计示意图的几何表述方式建立联系，数字标识清楚，不需要数学化表述，也不需要使用数学工具；设计问题解决策略注重的是要清楚周长信息，能从一些已知信息进行推断，答题中最核心的能力要求是推理

论证能力。图 B 的周长无法从图片信息中直接得知。图 B 中给出了平行四边形上下对边的长度，左右对边的长度需要通过推理计算才能得知，需要沿下方边长垂直做高、勾股定理进行推理得知，直角三角形斜边大于任意一个直角边，故图 B 中平行四边形左右两侧对边均长于 6m，加上上下对边边长和 20m，总周长是大于 32m，不符合题意。图 A、C、D 的周长可以从图片中已有信息推断，均符合题意：图 A 中与水平方向垂直的两侧边长的总长度没有告知，可以利用与水平面垂直的高的边长（6m），用符号、形式语言对图形进行适当填补，推理得出图 A 的周长为 32m。同理可以得到图 C 和图 D 的周长。PISA 测试中答对的学生低于 20.0%，A班学生在四个选项上判断正确率超过 70%，且对图A、C、D 判断正确率近 90.0%，明显高于参加 PISA

测试的学生的水平，可见我们的学生运用几何知识进行运算和解决生活中实际问题的能力是较强的。

（二）基于PISA测试分析框架和例题的几点思考

1. 重视对数学过程的考查

PISA 2012 年数学测评框架在 2003 年测评框架的基础上进行了适当调整，完善了数学素养内涵，

且将目标任务解决过程和数学基本能力有机整合，对于数学素养评定有了清晰的路径，能依据结果解释学生数学思维认知过程，意义是非常大的。我国的中高考数学测试中更侧重于知识和技能的测试，过程与方法维度测评相对较少，从国家学科测试框架顶层设计层面，应该进一步加强对 PISA 命题理念、测试分析框架和样题的分析，在数学素养测试方面加强数学“过程”的考查。

2. 重视对真实情境问题“数学化”的考查

PISA 非常重视考查学生将真实情境中的问题数学化，运用数学知识、技能去解决生活中的实际问题的能力，因此，题目都是从情境维度测评学生数学素养的，97.0%的 PISA 数学素养测试试题都是有真实情境的。我国学生的数学基础知识扎实，如果考查用数学语言来解决数学问题，学生的得分会很高，如例题 2、3，A 班学生答题正确率很高，远远高于 PISA 测试学生水平。可是现实世界中遇到的问题通常是具有不同表征形式的，并不一定都是用数学语言表达的，故此在数学教学中关注真实性问题情境的创设，强化现实问题向数学问题的思维转换训练，且提高学生对不同表征形式的数学问题的理解和转换能力，就显得尤为重要了。

3. 重视学生读图、提取信息能力的培养

PISA 数学测试重视对学生读图、认图、释图能力的考查，关注学生运用数学知识解决现实生活中的问题，故此测试题中多有图表类型的题目。21世纪是信息化快速发展的时代，学生在日常生活中经常会看到各式各样的图表或表格，学生是需要学会读图并能对图表内涵进行解读的能力的。从 A 班学生答题情况来看，例题 1 是以图表形式呈现任务目标，需要学生提取图表数据并进行分析、判断、计算和预测，第三小题学生答题正确率非常低，只有 43.75%，远远低于 PISA 测试学生水平，这说明教学中要加强学生读图、认图、释图能力培养，这也是学生适应信息化社会一种必备的基础。

4. 重视学生基于计算机的数学能力考查

PISA 2012 数学测试首次提供了基于计算机的测试，不仅能够测量学生的信息技术素养，同时还

大大减轻学生计算方面的负担。通过设置一些动态性、交互性的测试任务，考查学生用数学工具进行恰当地表达和交流的能力。这种测试方式得到了广泛的好评。我国的中学数学及其他学科测试，多注重纸笔测验，很少引入计算机测试。从 PISA2015中国国家中心组织的预测试情况来看，学生纸笔考试完成得非常好，计算机测试形式明显影响了答题速度和表达准确性，这与 2012 年上海学生基于计算机问题解决能力测试结果是一致的：上海学生与其他国家（地区）数学、阅读、科学成绩相当的学生相比，使用计算机解决问题的表现显著较低，这与学生在家庭和学校用电脑学习的情况有关。因此，中学数学教学中应适当加强数学工具（硬件、软件）的功能教学，关注让信息技术成为学生学习和生活的工具。教学中要多给学生提供实践型、开放型、研究型学习的机会，增强学生在不确定条件下解决问题的能力和意愿，加强为学生设计个性化的作业，鼓励学生完成基于计算机的研究性作业。总之，基于 PISA 数学测试分析框架的例题分析给我国数学素养评价、数学教学提供了诸多启示。借鉴 PISA 数学测试的理念和理论，可以丰富我国数学教育评价的研究。依据 PISA 测试数学过程与基本能力结合的框架，可以完善我国数学素养评价的工具，同时对于数学教学的改进、学生数学素养的提升都有重要的价值。

[参考文献]

[1] OECD2013.PISA 2012Mathematics Framework.[EB/OL].http://www.oecd.org/pisa/pisaproducts/46961598.pdf.

[2] OECD2014. PISA 2012 Results: Creative Problem Solving Stu-

dent’s Skills In Tackling Real-life Problems. [EB/OL].http://

www.oecd.org/pisa/.

[3] 綦春霞.PISA 数学素养测评及其特点[J].数学通报.2009，（6）.

[4] 王鼎.PISA 数学测评核心能力运用启示 [J]. 外国中小学教

育.2014，（2）.

[5] 刘达，徐炜蓉，陈吉.基于 PISA2012 数学素养测评框架的试题

设计一例[J].外国中小学教育，2014，（1）.

[6] 穆晓东，李娜娜.PISA2012 数学测试的启示——基于“数量”这

一内容的比较分析，[J].外国中小学教育，2014，（3）.

[7] 熊建辉，俞可. 国际大规模教育评估的影响力——以 PISA，

TIMSS 和 PIRLS 为例[J].人民教育，2014，（2）.